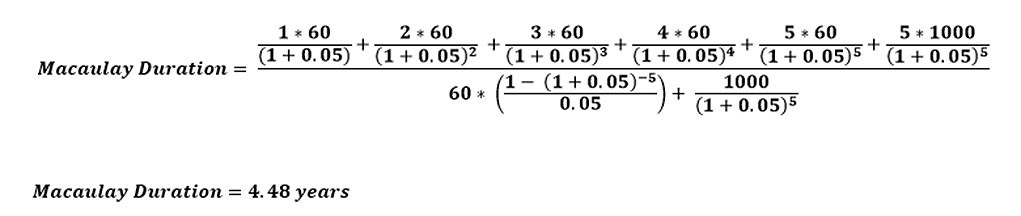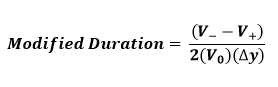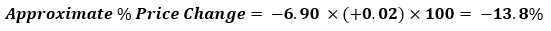If you own a bond or manage a bond portfolio, chances are that will you be following daily interest rates. You know that bond prices increase when rates rise, and decrease when rates fall. But how do you measure the bond’s price sensitivity to such rate fluctuations? The answer is duration.
Duration measures the percentage change in the price of a bond (or value of a bond portfolio) due to a change in market interest rates (also known as the yield).
Originally developed by Frederick Macaulay in 1938, it has become the standard measure of interest rate risk amongst practitioners in the fixed-income portfolio management profession, and has evolved into several variations used in the industry. Duration also plays an important role in bond immunization strategies.
Duration measures include Macaulay Duration, Modified Duration, Key Rate Duration, and Effective Duration.
Macaulay Duration
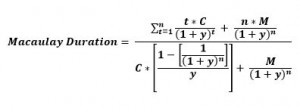
Being the first duration measure developed, it was defined by Frederick Macaulay as the present value of the weighted average term to maturity of cash flows from a bond, and as such was interpreted in temporal terms (number of years).
Formula
Where,
n = frequency of Coupon Payments
t = time to maturity
C = Coupon Payment
y = required yield
M = Maturity (or Par) Value
P = Bond’s Price
Note that the denominator in the above equation is the formula for determining the present value or price (P) of the bond.
Example
Assume a 5-Year bond paying a 6% annual coupon, and yielding 5%.Using the formula above, the bond’s Macaulay duration can be calculated as:
Modified Duration
Essentially an extension of Macaulay duration, modified duration is the predominant duration measure used in the fixed income industry, and is defined as the % price change (or price-sensitivity) of a bond to a 100 basis point change in yield.
Formula
where,
V0 = Bond’s Initial Price
V+ = Bond’s price if yields decrease by
V– = Bond’s price if yields increase by
= Change in yield (expressed in decimal)
YTM = Yield to Maturity (or Yield)
Example
To illustrate its calculation, a hypothetical bond will be used:
| Term to Maturity |
10 |
| Coupon Rate (annual) |
9% |
| Yield |
6% |
| Face Value |
$100 |
| Initial Bond Price |
$122.08 |
If we assume a 20 basis point change in yield modified duration can be calculated as:
Remember that this is the % price change for a 100 bps change in yield. Next, we show how to use this result to estimate the % price change for a yield shift of any magnitude.
Formula and Example for Estimating % Price Change Using Modified Duration
For example, assume that the yield for the bond above shifts from 6% to 8% (an increase of 200 basis points):
Therefore, a 200 bps increase in the yield will cause the price of the bond to approximately drop by 13.8%
Limitations of Modified Duration
We can see the first limitation of modified duration with the following graph:
Large shifts in yield will cause modified duration to be significantly inaccurate. Moreover, duration (as represented by the tangent line above), will underestimate bond prices with respect to yield shifts.
Another disadvantage is that modified duration does not account for option-embedded features in certain fixed-income securities (e.g., convertible bonds or mortgage-backed securities) which may cause future cash flows to change with shifts in yields.
Key-Rate Duration
Key-Rate Duration is computationally similar to Modified Duration, except that it accounts for non-parallel shifts in the yield curve. For example, the magnitude of a yield shift will differ for a 1-Year treasury compared to a 10 Year bond. Using key rate duration, we can assume non-parallel yield shifts across different maturities, thus obtaining a more accurate (and realistic) measure of interest rate exposure to a bond portfolio.
Effective Duration
This duration measure accounts for the embedded option features in certain fixed-income securities such as convertible securities or mortgage-backed securities, whose future cash flows could change with shifts in interest rates.
Conclusion
Duration measures the price-sensitivity of bonds due to changes in interest rates. It plays an important role in managing interest rate risk exposure. However, due to convexity issues, care must be taken when interpreting its results when assuming large shifts in the yield. Furthermore, when dealing with option-embedded bonds or an assumption of non-parallel yield shifts, effective duration and key-rate duration can provide better estimates of price sensitivity.
Key Words: Duration, Macaulay, Modified, Key Rate, Bond, Fixed-Income, Interest, Rate, Risk, Exposure, Yield, Term to Maturity, Coupon, Face Value, Principal, Price, Sensitivity, Percentage, Shift, Basis Points, Convexity